Dựa vào: Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right)\. Phân tích, đưa ra lời giải Giải bài 4 trang 124 sách bài tập toán 9 – Cánh diều tập 2 – Bài 1. Hình trụ. Tính diện tích toàn phần của mỗi hình trụ cho ở các hình 4a, 4b, 4c sau:…
Đề bài/câu hỏi:
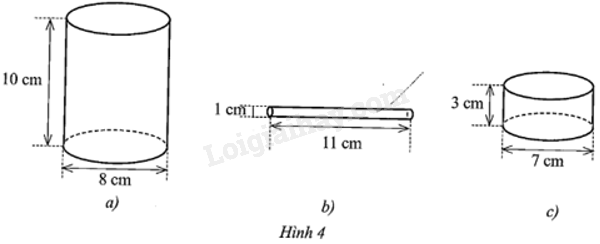
Tính diện tích toàn phần của mỗi hình trụ cho ở các hình 4a, 4b, 4c sau:
Hướng dẫn:
Dựa vào: Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right)\)
Lời giải:
Hình 4a):
Bán kính đáy của hình trụ là: 8 : 2 = 4 (cm).
Diện tích toàn phần của hình trụ là:
S = 2πr(r + h) = 2π.4.(4 + 10) = 112π ≈ 112.3,14 = 351,68 (cm2).
Hình 4b):
Bán kính đáy của hình trụ là: 1 : 2 = 0,5 (cm).
Diện tích toàn phần của hình trụ là:
S = 2πr(r + h) = 2π.0,5.(0,5 + 11) = 11,5π ≈ 11,5.3,14 = 36,11 (cm2).
Hình 4c):
Bán kính đáy của hình trụ là: 7 : 2 = 3,5 (cm).
Diện tích toàn phần của hình trụ là:
S = 2πr(r + h) = 2π.3,5.(3,5 + 3) = 45,5π ≈ 45,5.3,14 = 142,87 (cm2).
Vậy diện tích toàn phần ở các hình 4a, 4b, 4c lần lượt là: 351,68 cm2; 36,11 cm2; 142,87 cm2.