Bước 1: Thay tọa độ điểm A vào hàm số để tìm m, từ đó được công thức cụ thể của hàm số. Trả lời Giải bài 36 trang 72 sách bài tập toán 9 – Cánh diều tập 2 – Bài tập cuối Chương 7. Cho biết đồ thị hàm số (y = left( {m + 2} right){x^2}left( {m ne – 2} right)) đi qua…
Đề bài/câu hỏi:
Cho biết đồ thị hàm số \(y = \left( {m + 2} \right){x^2}\left( {m \ne – 2} \right)\) đi qua điểm \(A\left( { – 1; – 2} \right)\).
a) Tính giá trị của hàm số tại \(x = 3\).
b) Điểm \(B\left( {0,5; – 0,25} \right)\) có thuộc đồ thị hàm số hay không?
c) Tìm một số điểm thuộc đồ thị hàm số (khác điểm O) rồi vẽ đồ thị hàm số đó.
Hướng dẫn:
Bước 1: Thay tọa độ điểm A vào hàm số để tìm m, từ đó được công thức cụ thể của hàm số.
a) Bước 2: Thay \(x = 3\) vào hàm số vừa tìm được.
b) Bước 3: Thay hoành độ của B vào vế phải của hàm số rồi so sánh với tung độ của B: nếu giá trị vừa tìm được bằng tung độ của B thì B thuộc đồ thị hàm số và ngược lại.
c) Lấy giá trị x bất kì, từ đó tìm được y tương ứng (lấy ít nhất 4 giá trị).
Lời giải:
Đồ thị hàm số \(y = \left( {m + 2} \right){x^2}\left( {m \ne – 2} \right)\) đi qua điểm \(A\left( { – 1; – 2} \right)\) nên ta có:
\( – 2 = \left( {m + 2} \right){\left( { – 1} \right)^2}\) hay \( – 2 = m + 2\), suy ra \(m = – 4\) (thỏa mãn điều kiện).
Vậy hàm số có dạng \(y = \left( { – 4 + 2} \right){x^2}\) hay \(y = – 2{x^2}\)
a) Tại \(x = 3\), ta có \(y = – 2{x^2} = – {2.3^2} = – 18\).
Vậy \(x = 3\) thì hàm số có giá trị là \( – 18\).
b) Xét \(B\left( {0,5; – 0,25} \right)\): Với \(x = 0,5\) thì \( – 2{x^2} = – {2.0,5^2} = – 0,5 \ne 0,5\).
Vậy \(B\left( {0,5; – 0,25} \right)\) không thuộc đồ thị hàm số.
c) Bảng giá trị:

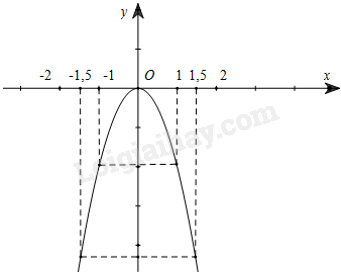
Đồ thị hàm số \(y = – 2{x^2}\) là đường parabol đi qua 5 điểm \(\left( { – 1,5; – 4,5} \right);\left( { – 1; – 2} \right);\left( {0;0} \right);\left( {1; – 2} \right);\left( {1,5; – 4,5} \right)\)