Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\). Hướng dẫn giải Giải bài 30 trang 135 sách bài tập toán 9 – Cánh diều tập 2 – Bài 3. Hình cầu. Một món đồ chơi có dạng như Hình 26….
Đề bài/câu hỏi:
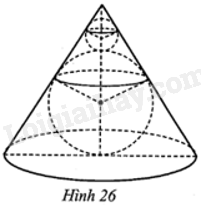
Một món đồ chơi có dạng như Hình 26. Vỏ ngoài món đồ chơi là một hình nón (bằng nhựa trong suốt) có bán kính đường tròn đáy là \(3\sqrt 3 \)cm và đường sinh là \(6\sqrt 3 \)cm. Trong hình nón là hai quả cầu (bằng thuỷ tinh) to và nhỏ, bán kính của chúng lần lượt là 3 cm và 1 cm. Tính tỉ số tổng thể tích của hai quả cầu và thể tích hình nón đó.
Hướng dẫn:
Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải:
Tổng thể tích của hai quả cầu là:
\(\frac{4}{3}\pi {.1^3} + \frac{4}{3}\pi {.3^3} = \frac{{112\pi }}{3}\) (cm3).
Ta có công thức tính độ dài đường sinh l qua chiều cao h và bán kính đáy r của hình nón là:
l2 = h2 + r2. Suy ra h2 = l2 – r2.
Khi đó, chiều cao của hình nón là:
\(\sqrt {{{\left( {6\sqrt 3 } \right)}^2} – {{\left( {3\sqrt 3 } \right)}^2}} = \sqrt {81} = 9\) (cm).
Thể tích hình nón là:
\(\frac{1}{3}.\pi .{\left( {3\sqrt 3 } \right)^2}.9 = 81\pi \) (cm3).
Tỉ số tổng thể tích của hai quả cầu và thể tích hình nón là:
\(\frac{{112\pi }}{3}:81\pi = \frac{{112}}{{243}}\)