Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\). Lời giải Giải bài 29 trang 135 sách bài tập toán 9 – Cánh diều tập 2 – Bài 3. Hình cầu. Người ta đổ đầy nước vào một bể hình lập phương cạnh 2a. Tiếp theo,…
Đề bài/câu hỏi:
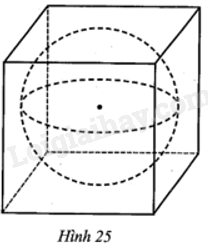
Người ta đổ đầy nước vào một bể hình lập phương cạnh 2a. Tiếp theo, người ta thả vào trong bể đó một vật thể có dạng hình cầu (đặc, không thấm nước) bán kính a như Hình 25. Hỏi lượng nước còn lại trong bể bằng bao nhiêu phần trăm lượng nước bị trào ra khỏi bể (làm tròn kết quả đến hàng phần mười)?
Hướng dẫn:
Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải:
Ta có lượng nước bị trào ra khỏi bể bằng thể tích hình cầu và bằng \(\frac{4}{3}\pi {a^3}\).
Thể tích của bể nước có dạng hình lập phương đó là: (2a)3 = 8a3.
Do đó, lượng nước còn lại trong bể là: \(8{a^3} – \frac{4}{3}\pi {a^3} = \frac{{\left( {24 – 4\pi } \right){a^3}}}{3}\).
Ta có tỉ số phần trăm của lượng nước còn lại trong bể và lượng nước bị trào ra khỏi bể là: \(\left[ {\frac{{\left( {24 – 4\pi } \right){a^3}}}{3}:\left( {\frac{4}{3}\pi {a^3}} \right)} \right].100\% \approx 91,1\% \).
Vậy lượng nước còn lại trong bể bằng khoảng 91,1% lượng nước bị trào ra khỏi bể.