Bước 1: Tính số đo góc B. Bước 2: Tính số đo cung nhỏ AB và BC (số đo cung gấp 2 lần số đo. Gợi ý giải Giải bài 30 trang 116 sách bài tập toán 9 – Cánh diều tập 1 – Bài 4. Góc ở tâm. Góc nội tiếp. Cho đường tròn (O) và ba điểm A, B,…
Đề bài/câu hỏi:
Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và \(\widehat {BAC} = 50^\circ \). So sánh các cung nhỏ AB, BC.
Hướng dẫn:
Bước 1: Tính số đo góc B.
Bước 2: Tính số đo cung nhỏ AB và BC (số đo cung gấp 2 lần số đo góc nội tiếp chắn cung đó).
Lời giải:
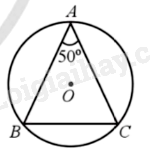
Do tam giác ABC cân tại A nên
\(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ – \widehat {BAC}}}{2} = \frac{{180^\circ – 50^\circ }}{2} = 65^\circ \).
Do đó số đo cung nhỏ AB là \(2.\widehat {ACB} = 65^\circ .2 = 130^\circ \)
Số đo cung nhỏ BC là \(2.\widehat A = 50^\circ .2 = 100^\circ \).
Vì \(130^\circ > 100^\circ \) nên cung nhỏ AB lớn hơn cung nhỏ BC.