Dựa vào: Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc. Chứng minh KH. Trả lời Giải bài 29 trang 92 sách bài tập toán 9 – Cánh diều tập 2 – Bài tập cuối Chương 8. Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh: a) Các tứ giác AKIB,…
Đề bài/câu hỏi:
Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh:
a) Các tứ giác AKIB, BLKC là các tứ giác nội tiếp.
b) Trực tâm H của tam giác ABC là tâm đường tròn nội tiếp tam giác IKL.
Hướng dẫn:
Dựa vào: Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc.
Chứng minh KH, LH là đường phân giác của góc LKI nên H tâm đường tròn nội tiếp tam giác IKL.
Lời giải:
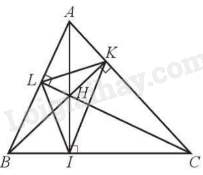
a) Ta có \(\widehat {AKB} = \widehat {AIB} = {90^o}\) (BK, AI là đường cao)
Tứ giác AKIB là các tứ giác nội tiếp (Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc).
Ta có \(\widehat {BLC} = \widehat {BKC} = {90^o}\)(LC, BK là đường cao)
Tứ giác BLKC là các tứ giác nội tiếp
b) Do tứ giác AKIB nội tiếp đường tròn nên \(\widehat {IKC} = \widehat {ABI}( = {180^o} – \widehat {AKI})\) hay \(\widehat {IKC} = \widehat {ABC}\). Tương tự \(\widehat {AKL} = \widehat {ABC}\). Suy ra \(\widehat {AKL} = \widehat {IKC}\).
Từ đó ta có \({90^o} – \widehat {AKL} = {90^o} – \widehat {IKC}\) hay \(\widehat {LKH} = \widehat {IKH}\). Vì vậy KH là đường phân giác của góc LKI. Tương tự cũng có LH là đường phân giác của góc KLI.
Vậy H tâm đường tròn nội tiếp tam giác IKL.