Phân tích: Quãng đường ngắn nhất mà chất điểm đó di chuyển là đi thẳng theo đoạn thẳng A’C. Tính A’C. Vận dụng kiến thức giải Giải bài 28 trang 61 sách bài tập toán 9 – Cánh diều tập 1 – Bài 3. Căn thức bậc hai và căn thức bậc ba của biểu thức đại số. Một chất điểm di chuyển từ định A’ đến đỉnh C trên bề mặt của hình lập phương ABCD….
Đề bài/câu hỏi:
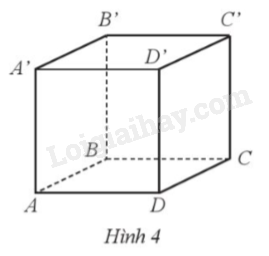
Một chất điểm di chuyển từ định A’ đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). Quãng đường ngắn nhất mà chất điểm đó di chuyển là bao nhiêu decimét?
Hướng dẫn:
Phân tích: Quãng đường ngắn nhất mà chất điểm đó di chuyển là đi thẳng theo đoạn thẳng A’C.
Tính A’C: Dựa vào định lý Pythagore trong tam giác vuông AA’C.
Lời giải:
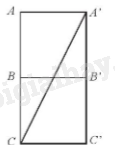
Giả sử chất điểm đó đi qua các mặt ABB’A’ và BCC’B’ của hình lập phương (các mặt khác tương tự). Trên đây là hình triển khai của các mặt ABB’A’ và BCC’B.
Tam giác AA’C vuông tại A nên áp dụng định lý Pythagore ta có:
\(A'{C^2} = AA{‘^2} + A{C^2} = AA{‘^2} + {\left( {AB + BC} \right)^2} = {1^2} + {\left( {1 + 1} \right)^2} = 5\)
Do đó \(A’C = \sqrt 5 dm\).
Vậy quãng đường ngắn nhất mà chất điểm đó di chuyển là \(\sqrt 5 dm.\)