Bước 1: Tính diện tích bức tường hình thang vuông. Bước 2: Tính diện tích cửa sổ. Bước 3. Hướng dẫn cách giải/trả lời Giải bài 23 trang 21 sách bài tập toán 9 – Cánh diều tập 1 – Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn. Một cửa số có dạng hình chữ nhật được xây trên bức tường có dạng hình thang vuông với các…
Đề bài/câu hỏi:
Một cửa số có dạng hình chữ nhật được xây trên bức tường có dạng hình thang vuông với các kích thước như Hình 4. Tìm x, y, biết rằng diện tích của bức tưởng không tính phần làm cửa sổ là 69 m2 và 2x = y – 3.
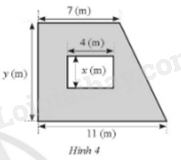
Hướng dẫn:
Bước 1: Tính diện tích bức tường hình thang vuông.
Bước 2: Tính diện tích cửa sổ.
Bước 3: Diện tích bức tường không có cửa sổ = diện tích hình thang vuông – diện tích cửa sổ (lập phương trình).
Bước 4: Rút y từ phương trình đã cho, thế vào phương trình vừa lập được.
Bước 5: Giải phương trình và đối chiếu điều kiện.
Lời giải:
Diện tích bức tường hình thang vuông là: \(\frac{{\left( {7 + 11} \right)y}}{2}\left( {{m^2}} \right).\)
Diện tích cửa sổ là: \(4x\left( {{m^2}} \right).\)
Do diện tích phần còn lại là 69m2 nên ta có phương trình \(\frac{{\left( {7 + 11} \right)y}}{2} – 4x = 69\) hay \(9y – 4x = 69\) (1).
Từ phương trình \(2x = y – 3\) ta có \(y = 2x + 3\) (2).
Thế (2) vào (1) ta được \(9\left( {2x + 3} \right) – 4x = 69\)
Giải phương trình trên:
\(\begin{array}{l}18x + 27 – 4x = 69\\14x = 42\\x = 3\end{array}\)
Thay \(x = 3\) vào phương trình (2) ta được \(y = 2.3 + 3 = 9\).
Vậy \(x = 3,y = 9\) là các giá trị cần tìm.