Chứng minh tứ giác EFGH và tứ giác IKPQ là hình vuông nên nội tiếp đường tròn. Phân tích, đưa ra lời giải Giải bài 21 trang 91 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Tứ giác nội tiếp đường tròn. Hình vuông ABCD có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp của nó để tạo…
Đề bài/câu hỏi:
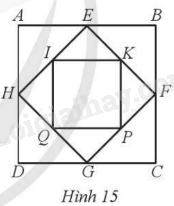
Hình vuông ABCD có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp của nó để tạo thành tứ giác EFGH, tiếp tục như vậy được tứ giác mới IKPQ (Hình 15). Chứng minh:
a) Tứ giác EFGH và tứ giác IKPQ là các tứ giác nội tiếp đường tròn.
b) Tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH bằng tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ.
Hướng dẫn:
Chứng minh tứ giác EFGH và tứ giác IKPQ là hình vuông nên nội tiếp đường tròn.
Dựa vào bán kính đường tròn ngoại tiếp hình vuông là trung điểm của cạnh huyền.
Lời giải:
a) Do ABCD là hình vuông nên AB = BC = CD = DA và \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\).
Do E, F,G,H lần lượt trung điểm của AB, BC, CD, DA nên AE = EB = BF = FC = CG = GD = DH = HA.
Xét tam giác AHE và tam giác BFE có
\(\widehat A = \widehat B = {90^o}\)
AH = BF
AE = BE
Do đó, \(\Delta AHE = \Delta BFE\) (hai cạnh góc vuông)
Suy ra HE = FE
Tương tự, ta chứng minh được HE = EF = FG =GH.
Khi đó, tứ giác EFGH là hình thoi.
Xét tam giác AHE có \(\widehat A = {90^o}\) và AH = AE nên tam giác AHE vuông cân tại A, suy ra \(\widehat {AEH} = {45^o}\). Tương tự, ta có \(\widehat {BEF} = {45^o}\).
Do đó \(\widehat {HEF} = {180^o} – \widehat {AEH} – \widehat {BEF} = {180^o} – {45^o} – {45^o} = {90^o}\).
Như vậy, hình thoi EFGH là hình vuông. Suy ra EFGH nội tiếp đường tròn.
Chứng minh tương tự ta được tứ giác IKPQ là hình vuông và nội tiếp đường tròn.
b) Xét ∆ABC vuông cân tại B (do và BA = BC) , theo định lí Pythagore, ta có: AC2 = AB2 + BC2 = AB2 + AB2 = 2AB2.
Suy ra AC = AB\(\sqrt 2 \). Bán kính đường tròn ngoại tiếp hình vuông ABCD là: \({R_1} = \frac{{AC}}{2} = \frac{{AB\sqrt 2 }}{2}\).
Tương tự, với ∆AHE vuông cân tại A, ta có: HE = AE\(\sqrt 2 \) = \(\frac{{AB\sqrt 2 }}{2}\).
Với ∆HEF vuông cân tại E, ta có:
\(HF = HE\sqrt 2 = \frac{{AB\sqrt 2 }}{2}.\sqrt 2 = AB\).
Bán kính đường tròn ngoại tiếp hình vuông EFGH là: \({R_2} = \frac{{HF}}{2} = \frac{{AB}}{2}\).
Chứng minh tương tự, ta có bán kính đường tròn ngoại tiếp hình vuông IKPQ là
\({R_3} = \frac{{IP}}{2} = \frac{{IK\sqrt 2 }}{2} = \frac{{IE\sqrt 2 .\sqrt 2 }}{2} = IE = \frac{{HE}}{2} = \frac{{\frac{{AB\sqrt 2 }}{2}}}{2} = \frac{{AB\sqrt 2 }}{4}.\)
Ta có tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH là:
\(\frac{{{R_1}}}{{{R_2}}} = \frac{{\frac{{AB\sqrt 2 }}{2}}}{{\frac{{AB}}{2}}} = \frac{{\sqrt 2 }}{2}.2 = \sqrt 2 \)
Tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ là:
\(\frac{{{R_2}}}{{{R_3}}} = \frac{{\frac{{AB}}{2}}}{{\frac{{AB\sqrt 2 }}{2}}} = \frac{1}{2}.\frac{4}{{\sqrt 2 }} = \sqrt 2 \).
Vậy tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH bằng tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ.