Bước 1: Kẻ đường cao AH. Bước 2: Áp dụng tỉ số lượng giác trong tam giác ABH để tình BH. Bước 3. Giải chi tiết Giải bài 21 trang 88 sách bài tập toán 9 – Cánh diều tập 1 – Bài 3. Ứng dụng của tỉ số lượng giác của góc nhọn. Bạn Hoa vẽ mặt cắt đứng phần mái của một ngôi nhà có dạng tam giác cân ABC (mái hai…
Đề bài/câu hỏi:
Bạn Hoa vẽ mặt cắt đứng phần mái của một ngôi nhà có dạng tam giác cân ABC (mái hai dốc). Biết rằng góc tạo bởi phần mái nhà và mặt phẳng nằm ngang là \(\widehat {ABC} = 25^\circ \) và độ dài mỗi bên dốc mái là 3,5m (hình 21). Tính độ dài đoạn thẳng BC (làm tròn kết quả đến hàng phần mười của mét).
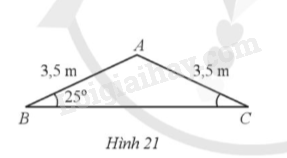
Hướng dẫn:
Bước 1: Kẻ đường cao AH.
Bước 2: Áp dụng tỉ số lượng giác trong tam giác ABH để tình BH.
Bước 3: Tính \(BC = 2BH\).
Lời giải:
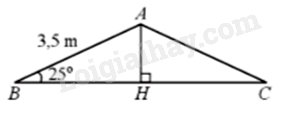
Kẻ đường cao AH của tam giác ABC.
Xét tam giác ABC vuông tại H có \(\cos B = \frac{{BH}}{{BA}}\)
suy ra \(BH = BA.\cos B = 3,5.\cos 25^\circ \).
Do tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến,
do đó \(BC = 2BH = 2.3,5.\cos 25^\circ \approx 6,3\)m.
vậy \(BC \approx 6,3\)m.