Diện tích xung quanh = 3. diện tích 1 mặt. b) Bước 1: Lập được phương trình biến x: Diện tích xung quanh = 36. Hướng dẫn giải Giải bài 21 trang 66 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Phương trình bậc hai một ẩn. Lập công thức tính diện tích xung quanh của một hình chóp tam giác đều,…
Đề bài/câu hỏi:
a) Lập công thức tính diện tích xung quanh của một hình chóp tam giác đều, biết độ dài cạnh đáy là x (dm) và độ dài trung đoạn là (x+2) (dm).
b) Tìm x để diện tích xung quanh của hình chóp tam giác đều đó là \(36d{m^2}.\)
Hướng dẫn:
a) Diện tích xung quanh = 3.diện tích 1 mặt.
b) Bước 1: Lập được phương trình biến x: Diện tích xung quanh = 36.
Bước 2: Giải phương trình và đối chiếu điều kiện.
Lời giải:
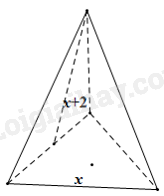
a) Vì 3 mặt của hình chóp tam giác đều là các tam giác cân bằng nhau nên diện tích xung quanh là:
\(3.\frac{1}{2}x.\left( {x + 2} \right) = \frac{3}{2}{x^2} + 3\) dm2.
b) Diện tích xung quanh của hình chóp tam giác đều là \(36d{m^2}\) nên ta có:
\(\frac{3}{2}{x^2} + 3 = 36\) hay \({x^2} + 2 – 24 = 0\)
suy ra \(\left( {x – 4} \right)\left( {x + 6} \right) = 0\).
Giải phương trình trên ta được \(x = 4;x = – 6\).
Ta thấy \(x = 4\) thỏa mãn điều kiện.
Vậy \(x = 4\).