Bước 1: Tính diện tích vải đỏ qua a. Bước 2: Tính diện tích vải xanh qua a. Bước 3. Hướng dẫn giải Giải bài 20 trang 66 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Phương trình bậc hai một ẩn. Một hộp quà thiết kế theo dạng hình hộp chữ nhật….
Đề bài/câu hỏi:
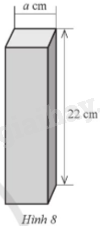
Một hộp quà thiết kế theo dạng hình hộp chữ nhật.
Bốn mặt thân hộp là các hình chữ nhật may bằng vải màu đỏ có chiều dài 22 cm, hai đáy hộp là các hình vuông cạnh a cm may bằng vải màu xanh (xem Hình 8). Tìm a để tổng diện tích vải màu đỏ nhiều hơn ba lần tổng diện tích vải màu xanh là 312 cm2, biết \(0 < a < 8\).
Hướng dẫn:
Bước 1: Tính diện tích vải đỏ qua a.
Bước 2: Tính diện tích vải xanh qua a.
Bước 3: Diện tích vải đỏ – 3. diện tích vải xanh = 312.
Bước 4: Giải phương trình và đối chiếu điều kiện.
Lời giải:
Diện tích vải màu đỏ là: \(4.22.a = 88a\) (cm2).
Diện tích vải màu xanh là: \(2{a^2}\) (cm2).
Do tổng diện tích vải màu đỏ nhiều hơn ba lần tổng diện tích vải màu xanh là 312 cm2 nên ta có:
\(88a – 3.2{a^2} = 312\)
hay \(3{a^2} – 44a + 156 = 0\)
suy ra \(\left( {3a – 26} \right)\left( {a – 6} \right) = 0\)
Giải phương trình trên ta được \(a = \frac{{26}}{3};a = 6\).
Đối chiếu điều kiện ta thấy \(a = 6\) thỏa mãn điều kiện. Vậy \(a = 6\).