Gọi M là trung điểm của BC. Áp dụng: Trong tam giác vuông. Vận dụng kiến thức giải Giải bài 20 trang 109 sách bài tập toán 9 – Cánh diều tập 1 – Bài 3. Tiếp tuyến của đường tròn. Cho đường tròn (O) và dây AB khác đường kính….
Đề bài/câu hỏi:
Cho đường tròn (O) và dây AB khác đường kính. Kẻ bán kính OC đi qua trung điểm I
của đoạn thẳng AB. Vẽ đường tròn (C; CI). Kẻ tiếp tuyến BD của đường tròn (C) với D là tiếp điểm và D khác I. Chứng minh:
a) Bốn đỉnh của tứ giác BDCI cùng nằm trên một đường tròn.
b) BD là tiếp tuyến của đường tròn (O).
Hướng dẫn:
a) Gọi M là trung điểm của BC.
Áp dụng: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1 nửa cạnh huyền (tam giác IBC và DBC) để suy ra \(MB = MC = MD = MI\).
b) Bước 1: Chứng minh \(\widehat {DCB} = \widehat {OBC}\left( { = \widehat {OCB}} \right)\).
Bước 2: \(\widehat {DCB} + \widehat {CBD} = \widehat {CBO} + \widehat {CBD} = \widehat {OBD} = 90^\circ \).
Lời giải:
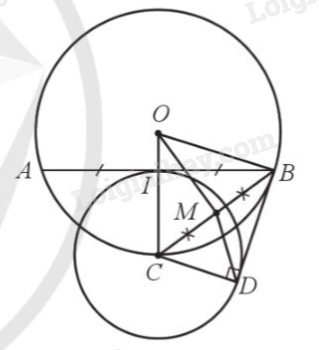
a) Xét tam giác OAB có: \(OA = OB\) (đều bằng bán kính (O)) nên tam giác OAB cân tại O, mà I là trung điểm của AB nên OI là đường trung tuyến đồng thời là đường cao của tam giác OAB, do đó \(OI \bot AB\).
Lấy M là trung điểm của CB nên DM, IM lần lượt là đường trung tuyến của 2 tam giác vuông IBC và DCB, nên ta có \(MB = MC = MD = MI = \frac{{BC}}{2}\).
Do đó 4 đỉnh của tứ giác BDCI cung nằm trên một đường tròn đường kính BC.
b) Để giải phương trình trên, ta giải 2 phương trình sau:
Xét tam giác OBC có \(OB = OC\)(cùng bằng bán kính (O)) nên \(\widehat {OCB} = \widehat {OBC}\) (1)
Xét (C; CI) có AB vuông góc với CI tại I nên AB là tiếp tuyến của (C; CI).
Mặt khác BD cũng là tiếp tuyến của (C;CI).
Suy ra \(\widehat {ICB} = \widehat {DCB}\) (2).
Từ (1) và (2) nên \(\widehat {DCB} = \widehat {OBC}\).
Ta lại có \(\widehat {DCB} + \widehat {DBC} = 90^\circ \) (do tam giác CBD vuông tại D) hay \(\widehat {OBC} + \widehat {DBC} = 90^\circ \), do đó \(\widehat {OBD} = 90^\circ \).
Suy ra \(BD \bot OB\) tại B.
Vậy BD là tiếp tuyến (O).