Dựa vào khoảng cách từ tâm I, J tới các điểm thuộc đường tròn bằng nhau suy ra các tứ giác AMBN. Hướng dẫn giải Giải bài 18 trang 91 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Tứ giác nội tiếp đường tròn. Cho (widehat {xAy} = {60^o}) và điểm B nằm trong góc xAy….
Đề bài/câu hỏi:
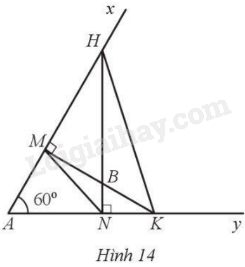
Cho \(\widehat {xAy} = {60^o}\) và điểm B nằm trong góc xAy. Kẻ đường thẳng BN vuông góc với Ay cắt Ax tại H; kẻ đường thẳng BM vuông góc với Ax cắt Ay tại K (Hình 14). Chứng minh:
a) Các tứ giác AMBN, HMNK là các tứ giác nội tiếp đường tròn.
b) HK = 2MN
Hướng dẫn:
Dựa vào khoảng cách từ tâm I, J tới các điểm thuộc đường tròn bằng nhau suy ra các tứ giác AMBN, HMNK là các tứ giác nội tiếp đường tròn.
Sử dụng tính chất tỉ số lượng giác để chứng minh.
Lời giải:
a) Gọi I; J lần lượt là trung điểm của AB, HK.
Khi đó MI, NI lần lượt là các đường trung tuyến ứng với cạnh huyền AB của các tam giác vuông AMB, ANB nên IM = IN = IA = IB = \(\frac{{AB}}{2}\).
Suy ra tứ giác AMBN nội tiếp đường tròn tâm I đường kính AB.
Tương tự tứ giác HMNK nội tiếp đường tròn tâm J đường kính HK.
b) Do tứ giác HMNK nội tiếp đường tròn nên \(\widehat {AMN} = \widehat {NKH} = ( = {180^o} – \widehat {HMN})\) hay \(\widehat {AMN} = \widehat {AKH}\).
Mà \(\widehat {MAN} = \widehat {KAH}\) suy ra \(\Delta AMN\backsim \Delta AKH\).
Do đó \(\frac{{HK}}{{MN}} = \frac{{AH}}{{AN}}\) (3).
Lại có tam giác AHN vuông tại N nên cos \(\widehat {HAN} = \frac{{AN}}{{AH}}\) hay cos 60o = \(\frac{{AN}}{{AH}}\), tức là \(\frac{{AN}}{{AH}} = \frac{1}{2}\).
Do đó AH = 2 AN (4). Từ (3) và (4) suy ra HK = 2 MN.