Dựa vào: Diện tích toàn phần hình nón: \({S_{xq}} = \pi rl + \pi {r^2} = \pi r\left( {l + r} \right)\). Gợi ý giải Giải bài 17 trang 130 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Hình nón. Cho hình chóp tam giác đều ABCD có các cạnh đáy và cạnh bên đều bằng a….
Đề bài/câu hỏi:
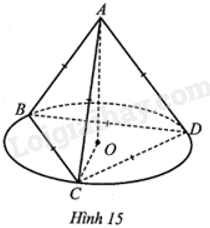
Cho hình chóp tam giác đều ABCD có các cạnh đáy và cạnh bên đều bằng a. Hình nón (N) có đỉnh A và đường tròn đáy tâm O là đường tròn ngoại tiếp tam giác BCD (Hình 15). Tính diện tích toàn phần của hình nón (N) đó theo a.
Hướng dẫn:
Dựa vào: Diện tích toàn phần hình nón: \({S_{xq}} = \pi rl + \pi {r^2} = \pi r\left( {l + r} \right)\).
Lời giải:
Vì ABCD là hình chóp tứ giác đều nên AB = AC = AD = BC = CD = DB = a.
Vì O là tâm của đường tròn ngoại tiếp ∆BCD nên bán kính R của đường tròn tâm O là \(R = \frac{{a\sqrt 3 }}{3}\).
Hình nón (N) có bán kính đáy là \(R = \frac{{a\sqrt 3 }}{3}\) và đường sinh là AB = a nên diện tích toàn phần của nó là: \(\pi .\frac{{a\sqrt 3 }}{3}.a + \pi .{\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = \frac{{\pi {a^2}(1 + \sqrt 3 )}}{3}\).