Chứng minh \(\widehat {AEB} = \widehat {AEC} = {60^o}\)suy ra EA là phân giác của góc BEC. Phân tích và giải Giải bài 16 trang 90 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Tứ giác nội tiếp đường tròn. Cho đường tròn (O) ngoại tiếp tam giác đều ABC….
Đề bài/câu hỏi:
Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Điểm E nằm trên cung nhỏ BC (E khác B và C). ED là tia đối của tia EB. Chứng minh EC là phân giác của góc AED và EA là phân giác của góc BEC.
Hướng dẫn:
Chứng minh \(\widehat {AEB} = \widehat {AEC} = {60^o}\)suy ra EA là phân giác của góc BEC.
Lời giải:
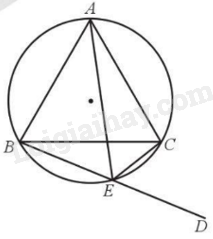
Ta có tứ giác ABEC nội tiếp đường tròn nên \(\widehat {CED} = \widehat {BAC} = {60^o}( = {180^o} – \widehat {BEC})\). Mặt khác \(\widehat {AEC} = \widehat {CED} = {60^o}\). Do đó, EC là phân giác của góc AED.
Tương tự ta có \(\widehat {AEC} = \widehat {ABC} = {60^o}\) và \(\widehat {AEB} = \widehat {ACB} = {60^o}\).
Do đó \(\widehat {AEB} = \widehat {AEC} = {60^o}\) hay EA là phân giác của góc BEC.