Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng 180o. Hướng dẫn giải Giải bài 15 trang 90 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Tứ giác nội tiếp đường tròn. Ở Hình 13, hai đường tròn (O), (O’) giao nhau tại A,…
Đề bài/câu hỏi:
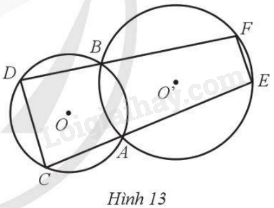
Ở Hình 13, hai đường tròn (O), (O’) giao nhau tại A, B và CD là một dây cung của (O). Tia CA cắt (O’) tại E và tia DB cắt (O’) tại F. Chứng minh EF song song với CD.
Hướng dẫn:
Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng 180o.
Lời giải:
Ta có tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat {ACD} = \widehat {ABF}( = {180^o} – \widehat {ABD})\) (1).
Mặt khác, tứ giác ABFE nội tiếp đường tròn (O’) suy ra \(\widehat {ABF} + \widehat {AEF} = {180^o}\) (2).
Từ (1) và (2) ta có \(\widehat {ACD} + \widehat {AEF} = {180^o}\) hay \(\widehat {ECD} + \widehat {CEF} = {180^o}\). Suy ra EF // CD.