Thứ tự hàng bằng số khối ở mỗi hàng, vì vậy tháp n tầng ta lập được tổng gồm n số hạng từ 1 đến. Hướng dẫn trả lời Giải bài 15 trang 65 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Phương trình bậc hai một ẩn. Ở một gian hàng của siêu thị, người ta xếp các khối hàng hình lập phương giống nhau thành hình…
Đề bài/câu hỏi:
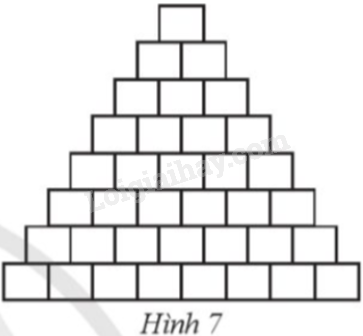
Ở một gian hàng của siêu thị, người ta xếp các khối hàng hình lập phương giống nhau thành hình tháp n tầng, với tầng đáy thứ n có n khối hàng, tầng ngay trên tầng đáy có (n − 1) khối hàng, …, tầng trên cùng có 1 khối hàng (chẳng hạn với n = 8 ta có cách xếp như minh hoạ ở Hình 7).
a) Tính tổng số S các khối hàng đã xếp ở một hình tháp n tầng.
b) Tìm n, biết S = 120.
Hướng dẫn:
a) Thứ tự hàng bằng số khối ở mỗi hàng, vì vậy tháp n tầng ta lập được tổng gồm n số hạng từ 1 đến n.
b) Từ công thức tìm được ở câu a, thay S = 120 vào ta tìm được n.
Lời giải:
a) Tổng số S các khối hàng đã xếp ở một hình tháp n tầng là:
\(S = 1 + 2 + 3 + … + \left( {n – 1} \right) + n = \frac{{n\left( {n + 1} \right)}}{2}\) khối hàng.
b) Với S = 120 ta có \(120 = \frac{{n\left( {n + 1} \right)}}{2}\) hay \(n\left( {n + 1} \right) = 240\), do đó \({n^2} + n – 240 = 0\).
Phương trình có các hệ số \(a = 1;b = 1;c = – 240\)
\(\Delta = {1^2} – 4.1.\left( { – 240} \right) = 961 > 0\)
Do \(\Delta > 0\) nên phương trình có 2 nghiệm phân biệt là:
\({n_1} = \frac{{ – 1 – \sqrt {961} }}{{2.1}} = – 16;{n_2} = \frac{{ – 1 + \sqrt {961} }}{{2.1}} = 15\)
Ta thấy \(n = – 16\) không thỏa mãn và \(n = 15\) thỏa mãn.
Vậy \(n = 15\) với S = 120.