Để vẽ đồ thị hàm số bậc hai ta cần lập bảng giá trị của hàm số đó. Vận dụng kiến thức giải Giải bài 10 trang 58 sách bài tập toán 9 – Cánh diều tập 2 – Bài 1. Hàm số y = ax² (a ≠ 0). Vẽ đồ thị các hàm số (y = – frac{3}{2}{x^2})và (y = frac{3}{2}{x^2})trên cùng một mặt phẳng toạ độ Oxy….
Đề bài/câu hỏi:
a) Vẽ đồ thị các hàm số \(y = – \frac{3}{2}{x^2}\) và \(y = \frac{3}{2}{x^2}\) trên cùng một mặt phẳng toạ độ Oxy.
b) Qua đồ thị của các hàm số đó, hãy cho biết khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số \(y = – \frac{3}{2}{x^2}\) và giá trị nhỏ nhất của hàm số \(y = \frac{3}{2}{x^2}\) là bao nhiêu?
Hướng dẫn:
– Để vẽ đồ thị hàm số bậc hai ta cần lập bảng giá trị của hàm số đó, cần ít nhất 5 giá trị để để vẽ đồ thị hàm số chuẩn hơn.
– Khi x tăng đồ thị hàm số đi lên tức là giá trị y tăng và ngược lại, do đó ta có thể dự đoán giá trị lớn nhất và giá trị nhỏ nhất
Lời giải:
a) Lập bảng giá trị của hàm số \(y = – \frac{3}{2}{x^2}\) ta được

Đồ thị hàm số \(y = – \frac{3}{2}{x^2}\) đi qua các điểm \(\left( {1; – \frac{3}{2}} \right);\) \(\left( { – 1; – \frac{3}{2}} \right);\) \(\left( {0;0} \right);\) \(\left( {2; – 6} \right);\) \(\left( { – 2; – 6} \right)\)
Lập bảng giá trị của hàm số \(y=\frac{3}{2}{{x}^{2}}\) ta được

Đồ thị hàm số \(y = \frac{3}{2}{x^2}\) đi qua các điểm \(\left( {1;\frac{3}{2}} \right);\) \(\left( { – 1;\frac{3}{2}} \right);\) \(\left( {0;0} \right);\) \(\left( {2;6} \right);\) \(\left( { – 2;6} \right)\)
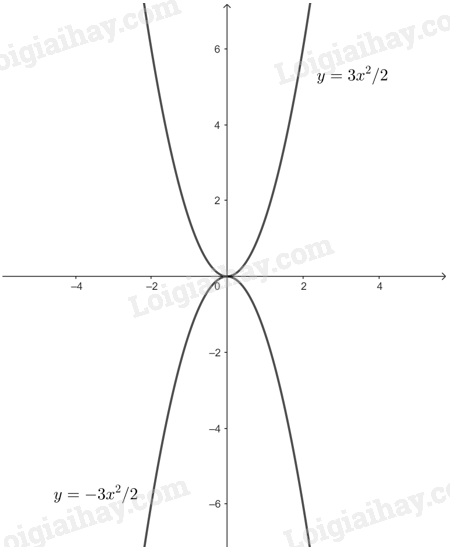
b) Qua đồ thị hàm số ta thấy khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số \(y = – \frac{3}{2}{x^2}\) lớn nhất tại \(x = 0,5\), khi đó \(y = – \frac{3}{2}.{\left( {0,5} \right)^2} = – \frac{3}{8}\).
Và khi x tăng từ 0,5 đến 2 thì giá trị nhỏ nhất của hàm số \(y = \frac{3}{2}{x^2}\) lớn nhất tại \(x = 0,5\), khi đó \(y = \frac{3}{2}.{\left( {0,5} \right)^2} = \frac{3}{8}\).