Sử dụng các tam giác đồng dạng để chứng minh. Trả lời Giải bài 8 trang 105 vở thực hành Toán 8 tập 2 – Bài tập cuối Chương 9. Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9….
Đề bài/câu hỏi:
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
a) \(\frac{B\text{D}}{BC}=\frac{AB}{AB+AC}\), từ đó suy ra \(A\text{E}=\frac{AB.AC}{AB+AC}\)
b) ΔDFC ∽ ΔABC
c) DF=DB
Hướng dẫn:
Sử dụng các tam giác đồng dạng để chứng minh
Lời giải:
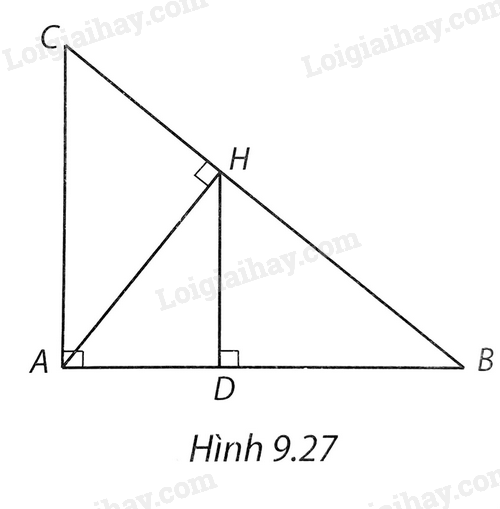
a) Hai tam giác vuông HDA (vuông tại D) và AHC (vuông tại H) có: $\widehat{DAH}={{90}^{0}}-\widehat{ACB}=\widehat{HCA}$.
Do đó $\Delta HDA\backsim \Delta AHC$ (cặp góc nhọn).
b) Áp dụng định lí Pythagore cho tam giác ABC vuông tại đỉnh A, ta có:
$B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}=41$, hay $BC=\sqrt{41}$ cm.
Mặt khác, trong tam giác vuông ABC với đường cao AH, ta có:
+) $AH.BC=2{{S}_{ABC}}=AB.AC$.
Do đó $AH=\frac{AB.AC}{BC}=\frac{20}{\sqrt{41}}$ (cm).
+) $A{{B}^{2}}=BH.BC$. Do đó $BH=\frac{A{{B}^{2}}}{BC}=\frac{25}{\sqrt{41}}$ (cm).
+) $A{{C}^{2}}=CH.BC$. Do đó $CH=\frac{A{{C}^{2}}}{BC}=\frac{16}{\sqrt{41}}$ (cm).
+ $HD=\frac{BH.AC}{BC}=\frac{\frac{25}{\sqrt{41}}.4}{\sqrt{41}}=\frac{100}{41}$ (cm).