Chứng minh tam giác GMN và tam giác GBC có NM // BC. Gợi ý giải Giải bài 7 trang 105 vở thực hành Toán 8 tập 2 – Bài tập cuối Chương 9. Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75)….
Đề bài/câu hỏi:
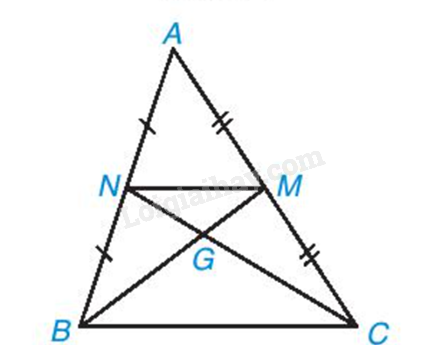
Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng
Hướng dẫn:
Chứng minh tam giác GMN và tam giác GBC có NM // BC
Lời giải:
Hai tam giác GMN và GBC có $\widehat{GMN}=\widehat{GBC},\widehat{BNM}=\widehat{GCB}$ (các cặp góc so le trong)
Do đó $\Delta GMN\backsim \Delta GBC$ (g.g) với tỉ số đồng dạng bằng $\frac{MN}{BC}=\frac{1}{2}$.