Dựa vào tính chất đường trung bình của tam giác. Hướng dẫn giải Giải bài 6 trang 81 vở thực hành Toán 8 – Bài tập cuối Chương 4. Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G….
Đề bài/câu hỏi:
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.
Hướng dẫn:
Dựa vào tính chất đường trung bình của tam giác.
Lời giải:
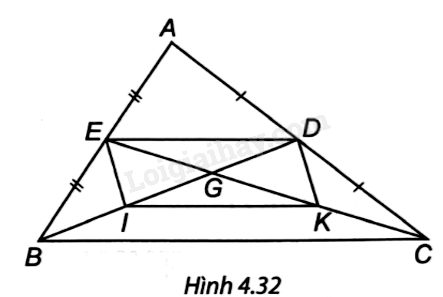
∆ABC có: E là trung điểm AB, D là trung điểm AC nên ED là đường trung bình của ∆ABC. Suy ra ED // BC và ED = \(\frac{1}{2}\)BC. (1)
∆GBC có: I là trung điểm GC, K là trung điểm GB nên IK là đường trung bình của ∆GBC. Suy ra IK // BC và IK = \(\frac{1}{2}\)BC. (2)
Từ (1) và (2) suy ra ED // IK và ED = IK nên tứ giác EDKI là hình bình hành.