Sử dụng tính chất của hình bình hành và tia phân giác của một góc. Vận dụng kiến thức giải Giải bài 3 trang 55 vở thực hành Toán 8 – Luyện tập chung trang 54. Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm….
Đề bài/câu hỏi:
Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.
a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
b) Tính khoảng cách từ giao điểm đó đến điểm C.
Hướng dẫn:
Sử dụng tính chất của hình bình hành và tia phân giác của một góc.
Lời giải:
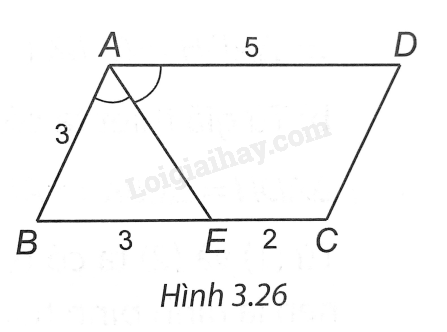
(H.3.26). a) Do ABCD là hình bình hành nên AD // BC, BC = AD = 5 cm.
Do BC = 5 cm nên có điểm E duy nhất trên cạnh BC sao cho BE = 3 cm.
Vì BE = AB ⇒ ∆BAE cân tại B \( \Rightarrow \widehat {BAE} = \widehat {BEA}.\) (1)
Do AD // BC \( \Rightarrow \widehat {BEA} = \widehat {EAD}\) (hai góc so le trong). (2)
Từ (1) và (2), ta có \(\widehat {BAE} = \widehat {EAD}\) hay tia AE là tia phân giác của góc BAD. Tia này không cắt cạnh CD.
b) Ta có EC = BC – BE = 5 – 3 = 2 (cm).