Chứng minh tứ giác AMCN là hình bình hành suy ra AN = CM (hai cạnh tương ứng). Hướng dẫn giải Giải bài 2 trang 55 vở thực hành Toán 8 – Luyện tập chung trang 54. Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM…
Đề bài/câu hỏi:
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
a) AN = CM.
b) \(\widehat {AMC} = \widehat {ANC}.\)
Hướng dẫn:
a) Chứng minh tứ giác AMCN là hình bình hành suy ra AN = CM (hai cạnh tương ứng).
b) Dựa vào tính chất của hình bình hành: Trong hình bình hành, hai góc đối bằng nhau.
Lời giải:
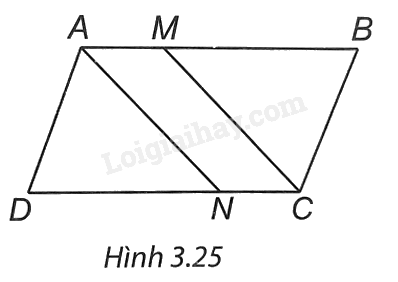
(H.3.25). a) ABCD là hình bình hành ⇒ AB // CD ⇒ AM // CN. Tứ giác AMCN có AM = CN, AM // CN ⇒ AMCN là hình bình hành.
⇒ AN = CM (hai cạnh đối của hình bình hành bằng nhau).
b) AMCN là hình bình hành \( \Rightarrow \widehat {AMC} = \widehat {ANC}\) (hai góc đối của hình bình hành bằng nhau).