Chứng minh dựa vào định lí Thales, Thales đảo và các trường hợp đồng dạng của hai tam giác. Lời giải Giải bài 14 trang 108 vở thực hành Toán 8 tập 2 – Bài tập cuối Chương 9. Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Các đường thẳng qua E,…
Đề bài/câu hỏi:
Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Các đường thẳng qua E, F lần lượt vuông góc và cắt CH, BH tại P, Q. Chứng minh rằng PQ // BC và $\Delta HPQ\backsim \Delta HEF$.
Hướng dẫn:
Chứng minh dựa vào định lí Thales, Thales đảo và các trường hợp đồng dạng của hai tam giác.
Lời giải:
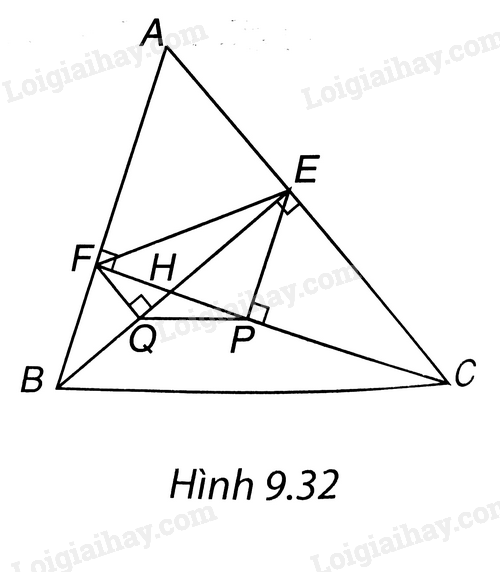
(H.9.32). Vì P // BF (cùng vuông góc với CF) nên theo định lí Thales ta có $\frac{HE}{HB}=\frac{HP}{HF}$, hay $HP=\frac{HE.HF}{HB}$.
Tương tự, vì FQ // CE (cùng vuông góc với BE) nên $\frac{HF}{HC}=\frac{HQ}{HE}$, hay $HQ=\frac{HE.HF}{HC}$. Do vậy $\frac{HP}{HQ}=\frac{HC}{HB}$.
Theo định lí Thales đảo ta suy ra PQ // BC.
Mặt khác, hai tam giác vuông BHF (vuông tại F) và CHE (vuông tại E) đồng dạng vì có một cặp góc nhọn bằng nhau là $\widehat{BHF}=\widehat{CHE}$ (hai góc đối đỉnh). Suy ra $\frac{HB}{HC}=\frac{HF}{HE}$.
Do vậy $\frac{HP}{HQ}=\frac{HC}{HB}=\frac{HE}{HF}$.
Hai tam giác HPQ và HEF có: $\frac{HP}{HQ}=\frac{HE}{HF}$ (theo chứng minh trên), $\widehat{PHQ}=\widehat{EHF}$ (hai góc đối đỉnh).
Do đó $\Delta HPQ\backsim \Delta HEF$ (c.g.c).