Sử dụng các tam giác đồng dạng để chứng minh. Gợi ý giải Giải bài 10 trang 106 vở thực hành Toán 8 tập 2 – Bài tập cuối Chương 9. Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9….
Đề bài/câu hỏi:
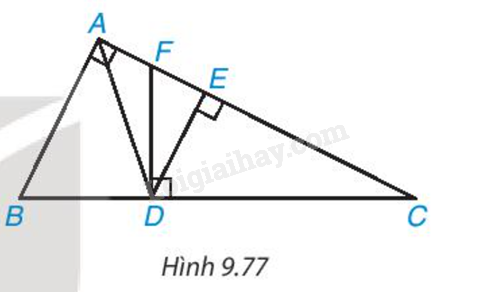
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
a) \(\frac{B\text{D}}{BC}=\frac{AB}{AB+AC}\), từ đó suy ra \(A\text{E}=\frac{AB.AC}{AB+AC}\);
b) ΔDFC ∽ ΔABC;
c) DF = DB
Hướng dẫn:
Sử dụng các tam giác đồng dạng để chứng minh.
Lời giải:
a) Kẻ đường thẳng qua D vuông góc và cắt AB tại K. Khi đó DK = AE.
Vì DE // AB, DK // AC nên $\Delta BDK\backsim \Delta BCA$ và $\Delta CDE\backsim \Delta CBA$.
Suy ra $\frac{BD}{BC}=\frac{DK}{CA}=\frac{DE}{CA}=\frac{DE}{BA}.\frac{BA}{CA}=\frac{DC}{BC}.\frac{AB}{AC}$.
Do vậy $BD=\frac{DC.AB}{AC}$ , hay $\frac{DC}{BD}=\frac{AB}{AC}$ (*)
Từ (*) suy ra $\frac{BC}{BD}=1+\frac{DC}{BD}=1+\frac{AC}{AB}=\frac{AB+AC}{AB}$, do đó $\frac{BD}{BC}=\frac{AB}{AB+AC}$.
Theo định lí Thalès, ta có: $\frac{AE}{AC}=\frac{BD}{BC}=\frac{AB}{AB+AC}$. Suy ra AE = \(\frac{AB.AC}{AB+AC}\).
b) Hai tam giác vuông DFC (vuông tại D) và ABC (vuông tại A) có góc nhọn C chung nên $\Delta DFC\backsim \Delta ABC$ suy ra $\frac{DF}{AB}=\frac{DC}{AC}=\frac{DC}{DB}.\frac{DB}{AC}=\frac{AC}{AB}.\frac{DB}{AC}=\frac{DB}{AB}$.
Do đó DF = DB.