Lời giải Thử thách nhỏ Bài 35. Định lí Pythagore và ứng dụng (trang 95, 96, 97) – SGK Toán 8 Kết nối tri thức. Hướng dẫn: Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC.
Câu hỏi/Đề bài:
Tính chiều cao theo đơn vị centimét của một tam giác đều cạnh 2cm (h.9.44) (làm tròn kết quả đến chữ số thập phân thứ hai)
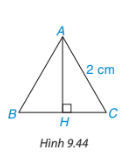
Hướng dẫn:
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC.
Áp đụng định lí Pythagore trong tam giác AHC suy ra độ dài của chiều cao
Lời giải:
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC suy ra
\(HB = HC = \frac{{BC}}{2} = \frac{2}{2} = 1\)(cm)
Áp đụng định lí Pythagore trong tam giác AHC ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} \Rightarrow A{H^2} = A{C^2} – H{C^2} = {2^2} – {1^2} = 3\\ \Rightarrow AH = \sqrt 3 \approx 1,73(cm)\end{array}\)
Vậy chiều cao của tam giác đều là 1, 73 cm