Trả lời Luyện tập 2 Bài 34. Ba trường hợp đồng dạng của hai tam giác (trang 85, 86, 87) – SGK Toán 8 Kết nối tri thức. Tham khảo: Áp đụng định lí trường hợp đồng dạng canh – góc – cạnh để chứng minh \(\Delta A’B’M’ \backsim \Delta.
Câu hỏi/Đề bài:
Cho ΔA’B’C’ ∽ ΔABC. Trên tia đối của các tia CB, C’B’ lần lượt lấy các điểm M, M’ sao cho \(\frac{{MC}}{{MB}} = \frac{{M’C’}}{{M’B’}}\). Chứng minh rằng ΔA’B’M’ ∽ ΔABM
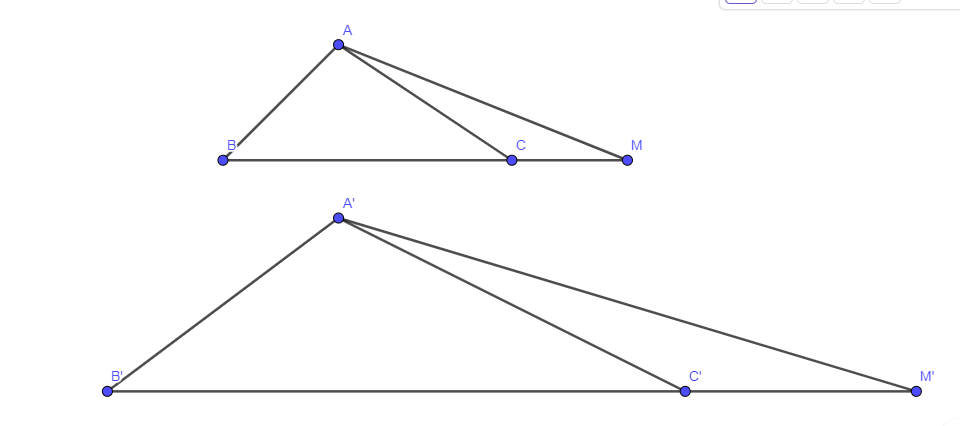
Hướng dẫn:
Áp đụng định lí trường hợp đồng dạng canh – góc – cạnh để chứng minh \(\Delta A’B’M’ \backsim \Delta ABM\)
Lời giải:
Ta có:
\(\begin{array}{l}\frac{{MC}}{{MB}} = \frac{{M’C’}}{{M’B’}}\\ \Rightarrow \frac{{MB – BC}}{{MB}} = \frac{{M’B’ – B’C’}}{{M’B’}}\\ \Rightarrow 1 – \frac{{BC}}{{MB}} = 1 – \frac{{B’C’}}{{M’B’}}\\ \Rightarrow \frac{{BC}}{{MB}} = \frac{{B’C’}}{{M’B’}}\\ \Rightarrow \frac{{M’B’}}{{MB}} = \frac{{B’C’}}{{BC}}(1)\end{array}\)
Vì ΔA’B’C’ ∽ ΔABC suy ra:
\(\begin{array}{l}\widehat {B’} = \widehat B\\\frac{{A’B’}}{{AB}} = \frac{{B’C’}}{{BC}}(2)\end{array}\)
Từ (1) và (2) suy ra:
\(\frac{{M’B’}}{{MB}} = \frac{{A’B’}}{{AB}}\)
Xét tam giác ABM và tam giác A”B”M’ có:
\(\begin{array}{l}\widehat {B’} = \widehat B\\\frac{{M’B’}}{{MB}} = \frac{{A’B’}}{{AB}}\end{array}\)
Suy ra \(\Delta A’B’M’ \backsim \Delta ABM\)