Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để chứng minh. Vận dụng kiến thức giải Giải bài 9.7 trang 90 SGK Toán 8 tập 2 – Kết nối tri thức – Bài 34. Ba trường hợp đồng dạng của hai tam giác. Cho AM, BN, CP là các đường trung tuyến của tam giác ABC…
Đề bài/câu hỏi:
Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A’M’, B’N’, C’P’ là các đường trung tuyến của tam giác A’B’C’. Biết rằng ΔA’B’C’ ∽ ΔABC
Chứng minh rằng \(\frac{{A’M’}}{{AM}} = \frac{{B’N’}}{{BN}} = \frac{{C’P’}}{{CP}}\)
Hướng dẫn:
Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để chứng minh.
Lời giải:
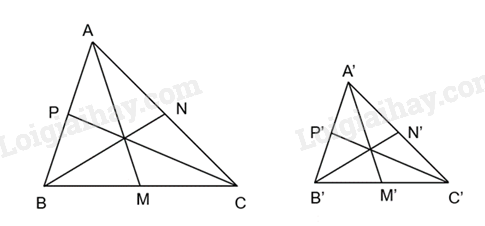
Vì ΔA’B’C’ ∽ ΔABC
=> ΔA’M’B’ ∽ ΔAMB
=> \(\frac{{A’M’}}{{AM}} = \frac{{A’B’}}{{AB}}(1)\) (1)
Vì \(\Delta A’B’C’\) ∽ ΔABC
=> Vì ΔA′B′N′ ∽ ΔABN
=> \(\frac{{B’N’}}{{BN}} = \frac{{A’B’}}{{AB}}\) (2)
Từ (1) và (2) => \(\frac{{A’M’}}{{AM}} = \frac{{B’N’}}{{BN}}\)(3)
Vì ΔA’B’C’ ∽ ΔABC
=> Vì ΔA’C’P’ ∽ ΔACP
=> \(\frac{{C’P’}}{{CP}} = \frac{{A’C’}}{{AC}}\) (4)
Vì ΔA′B′C′ ∽ ΔABC
=> ΔA′M′C′ ∽ ΔAMC
=> \(\frac{{A’M’}}{{AM}} = \frac{{A’C’}}{{AC}}\) (5)
Từ (4) và (5) => \(\frac{{C’P’}}{{CP}} = \frac{{A’M’}}{{AM}}\) (6)
Từ (3) và (6) => \(\frac{{A’M’}}{{AM}} = \frac{{B’N’}}{{BN}} = \frac{{C’P’}}{{CP}}\)