Bài 9.34 trang 109 Toán 8 tập 2 – Kết nối tri thức: Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC

Đề bài/câu hỏi:

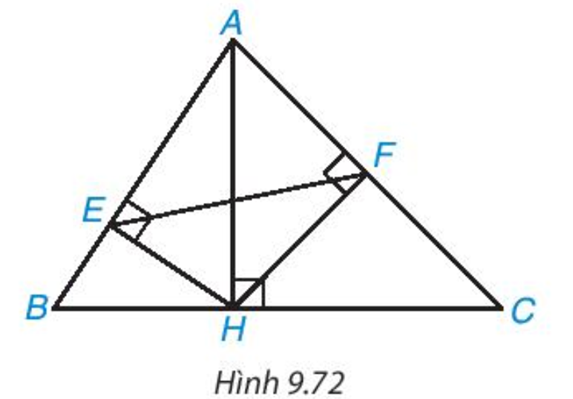
Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng

a) ΔAEH ∽ ΔAHB

b) ΔAFH ∽ ΔAHC

c) ΔAFE ∽ ΔABC

Hướng dẫn:

Sử dụng các trường hợp đồng dạng của tam giác vuông và tam giác thường.

Lời giải:

a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có: góc A chung

=> ΔAEH ∽ ΔAHB

b) Xét hai tam giác AFH (vuông tại F) và tam giác AHC (vuông tại H) có: góc A chung

ΔAFH ∽ ΔAHC

c) Vì ΔAEH ∽ ΔAHB nên:

\(\frac{{A{\rm{E}}}}{{AH}} = \frac{{AH}}{{AB}} \Rightarrow A{\rm{E}} = \frac{{A{H^2}}}{{AB}}\) (1)

Vì ΔAFH ∽ ΔAHC nên:

\(\frac{{AF}}{{AH}} = \frac{{AH}}{{AC}} \Rightarrow AF = \frac{{A{H^2}}}{{AC}}\)(2)

Từ (1) và (2) ta có:

\(\frac{{A{\rm{E}}}}{{AF}} = \frac{{AC}}{{AB}} \Rightarrow \frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\)

Xét hai tam giác ΔAFE và ΔABC có:

Góc A chung

\(\frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\)

Suy ra ΔAFE ∽ ΔABC (c.g.c)