Vì ΔA′B′C′ ∽ ΔABC => \(\widehat B = \widehat {B’};\frac{{A’H’}}{{AB}} = \frac{{A’C’}}{{AC}} = \frac{{B’C’}}{{BC}} = k\. Lời giải Giải bài 9.27 trang 103 SGK Toán 8 tập 2 – Kết nối tri thức – Bài 36. Các trường hợp đồng dạng của hai tam giác vuông. Cho tam giác A’B’C’ đồng dạng với tam giác ABC…
Đề bài/câu hỏi:
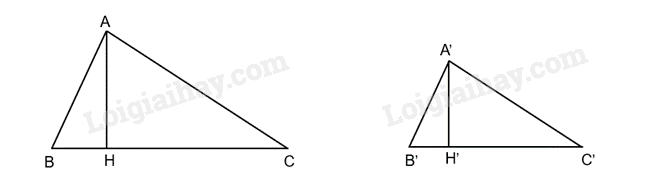
Cho tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k. Gọi A’H’ và AH lần lượt là các đường cao đỉnh A’ và A của tam giác A’B’C’ và tam giác ABC. Chứng minh rằng:
a) \(\frac{{A’H’}}{{AH}} = k\)
b) Diện tích tam giác A’B’C’ bằng \(k^2\) lần diện tích tam giác ABC
Hướng dẫn:
a) Vì ΔA′B′C′ ∽ ΔABC
=> \(\widehat B = \widehat {B’};\frac{{A’H’}}{{AB}} = \frac{{A’C’}}{{AC}} = \frac{{B’C’}}{{BC}} = k\)
Chứng minh ΔA′H′B′ ∽ ΔAHB suy ra các hệ số tỉ lệ và chứng minh được \(\frac{{A’H’}}{{AH}} = k\)
b) Tính diện tích tam giác ABC và A”B”C” từ đó sẽ xét tỉ số diện tích của hai tam giác đó.
Lời giải:
a) Vì ΔA′B′C′ ∽ ΔABC
=> \(\widehat B = \widehat {B’};\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}} = \frac{{B’C’}}{{BC}} = k\)
Xét hai tam giác vuông A’H’B’ (vuông tại H’) và tam giác vuông AHB (vuông tại H), có:
\(\widehat B = \widehat {B’}\)
=> ΔA′H′B′ ∽ ΔAHB
=> \(\frac{{A’H’}}{{AH}} = \frac{{A’B’}}{{AB}}\)
Mà \(\frac{{A’B’}}{{AB}} = k\)
=> \(\frac{{A’H’}}{{AH}} = k\)
b) Có diện tích tam giác ABC là: \(\frac{1}{2}\)AH.BC
Có diện tích tam giác A’B’C’ là: \(\frac{1}{2}\)A′H′.B′C′
Xét tỉ lệ giữa hai tam giác A’B’C’ và tam giác ABC có:
\(\frac{{\frac{1}{2}A’H’.B’C’}}{{\frac{1}{2}AH.BC}} = \frac{{A’H’}}{{AH}}.\frac{{B’C’}}{{BC}} = k.k = {k^2}\)