Bài 4.3 trang 80 Toán 8 tập 1 – Kết nối tri thức: Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại

Đề bài/câu hỏi:

Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.

Chứng minh rằng: \(\dfrac{{A{\rm{E}}}}{{AB}} + \dfrac{{AF}}{{AC}} = 1\)

Hướng dẫn:

Áp dụng định lí Thalès trong tam giác ABC, ta có các tỉ lệ thức. Áp dụng dãy tỉ số bằng nhau ta được đpcm.

Lời giải:

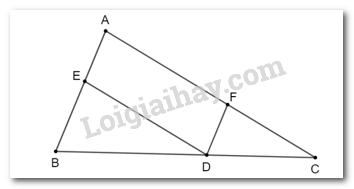
Áp dụng định lí Thalès, ta có:

• Vì DE // AC nên \(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{C{\rm{D}}}}{{BC}}\)

• Vì DF // AC nên \(\dfrac{{AF}}{{AC}} = \dfrac{{B{\rm{D}}}}{{BC}}\)

Khi đó, \(\dfrac{{A{\rm{E}}}}{{AB}} + \dfrac{{AF}}{{AC}} = \dfrac{{C{\rm{D}}}}{{BC}} + \dfrac{{B{\rm{D}}}}{{BC}} = 1\) (đpcm).