Bài 3.32 trang 72 Toán 8 tập 1 – Kết nối tri thức: Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật

Đề bài/câu hỏi:

Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.

Hướng dẫn:

Giả sử ABCD là hình thoi. Gọi E, H, G, F lần lượt là trung điểm của các cạnh AB; AD; DC; CB.

Chứng minh các cặp cạnh song song và bằng nhau suy ra EFGH là hình chữ nhật.

Lời giải:

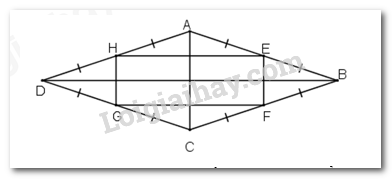
Ta cần chứng minh EFGH là hình chữ nhật. Thật vậy:

Do ABCD là hình thoi nên AB = BC = CD = DA.

Do E, H lần lượt là trung điểm của AB, AD nên AH = DH = AE = BE.

Tam giác AHE có AH = AE nên là tam giác cân tại A, suy ra \(\widehat {AHE} = \widehat {AEH}\)

Mà \(\widehat {HAE} + \widehat {AHE} + \widehat {AEH} = 180^\circ \)

Suy ra \(\widehat {AHE} = \frac{{180^\circ – \widehat {HAE}}}{2}\)

Tương tự, ta có tam giác DHG cân tại D nên \(\widehat {DHG} = \frac{{180^\circ – \widehat {HDG}}}{2}\)

Mặt khác, do ABCD là hình thoi nên AB // CD, suy ra \(\widehat {HAE} + \widehat {HDG} = 180^\circ \)

Khi đó \(\widehat {AHE} + \widehat {DHG} = \frac{{180^\circ – \widehat {HAE}}}{2} + \frac{{180^\circ – \widehat {HDG}}}{2}\)

= \(\frac{{180^\circ – \widehat {HAE} + 180^\circ – \widehat {HDG}}}{2}\)

=\(\frac{{360^\circ – (\widehat {HAE} + \widehat {HDG})}}{2}\)

= \(\frac{{360^\circ – 180^\circ }}{2}\)

Mà \(\widehat {AHE} + \widehat {DHG} + \widehat {EHG} = 180^\circ \)

Suy ra \(\widehat {EHG} = 180^\circ – (\widehat {AHE} + \widehat {DHG}) = 180^\circ – 90^\circ = 90^\circ \)

Chứng minh tương tự như trên ta cũng có \(\widehat {HEF} = \widehat {EFG} = \widehat {FGH} = {90^0}.\)

Tứ giác EFGH có bốn góc vuông nên là hình chữ nhật.