Giả sử ABCD là hình chữ nhật. Gọi E, H, G, F lần lượt là trung điểm của các cạnh AB; AD; DC; CB. Hướng dẫn giải Giải bài 3.31 trang 72 SGK Toán 8 tập 1 – Kết nối tri thức – Bài 14. Hình thoi và hình vuông. Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình…
Đề bài/câu hỏi:
Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.
Hướng dẫn:
Giả sử ABCD là hình chữ nhật. Gọi E, H, G, F lần lượt là trung điểm của các cạnh AB; AD; DC; CB.
Chứng minh các cạnh bằng nhau suy ra EFGH là hình thoi
Lời giải:
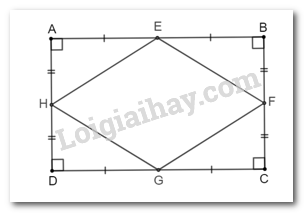
Xét các tam giác AEH, BEF, CGF, DGH có:
\( \widehat A = \widehat B = \widehat C = \widehat D = 90^0\)
AE = BE = CG = DG (vì E, G là trung điểm của AB, CD và AB = CD)
BF = FC = DH = HA (vì F, H là trung điểm của BC, AD và BC = AD)
\( \Rightarrow \Delta AEH = \Delta BEF = \Delta CGF = \Delta DGH \)
Suy ra EH = EF = FG = GH (các cạnh tương ứng) nên tứ giác EFGH là hình thoi (vì có 4 cạnh bằng nhau).