Sử dụng các tính chất của hình bình hành + Các cạnh đối bằng nhau + Các góc đối bằng nhau + Hai đường chéo. Giải chi tiết Giải bài 3.15 trang 61 SGK Toán 8 tập 1 – Kết nối tri thức – Bài 12. Hình bình hành. Cho hình bình hành ABCD….
Đề bài/câu hỏi:
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Chứng minh BF = DE.
Hướng dẫn:
Sử dụng các tính chất của hình bình hành
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Lời giải:
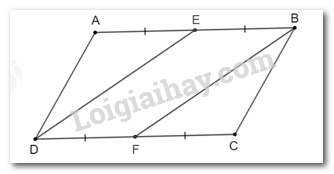
Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE, CF = DF.
Do đó AE = BE = CF = DF.
Xét tứ giác BEDF có:
BE = DF (chứng minh trên);
BE // DF (vì AB // CD)
Do đó tứ giác BEDF là hình bình hành.
Suy ra BF = DE (đpcm).