Giải Vận dụng 3 Bài 3. Hàm số bậc nhất y=ax+b(a≠0) (trang 18, 19, 20, 21) – SGK Toán 8 Chân trời sáng tạo. Tham khảo: Độ dài của lò xo sau khi treo vật nặng bằng độ dài ban đầu của lò xo cộng với.
Câu hỏi/Đề bài:
Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là 10 cm. Cho biết treo thêm vào lò xo 1 vật nặng 1 kg thì chiều dài lò xo tăng thêm 3 cm.
a) Tính chiều dài \(y\) (cm) của lò xo theo khối lượng \(x\) (kg) của vật.
b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).
Hướng dẫn:
Độ dài của lò xo sau khi treo vật nặng bằng độ dài ban đầu của lò xo cộng với độ dài tăng thêm do bị ảnh hưởng của vật nặng.
Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ – b}}{a}\) ta được điểm \(N\left( {\dfrac{{ – b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).
Lời giải:
Vì cứ treo thêm 1 kg vật nặng thì lò xo dài thêm 3 cm nên treo thêm \(x\) kg vật nặng thì lò xo dài thêm \(3x\) cm.
Chiều dài của lò xo sau khi treo vật nặng là:
\(y = 3x + 10\).
b) Vẽ đồ thị hàm số \(y = 3x + 10\)
Cho \(x = 0 \Rightarrow y = 10\) ta được điểm \(M\left( {0;10} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ – 10}}{3}\) ta được điểm \(N\left( {\dfrac{{ – 10}}{3};0} \right)\) trên \(Ox\).
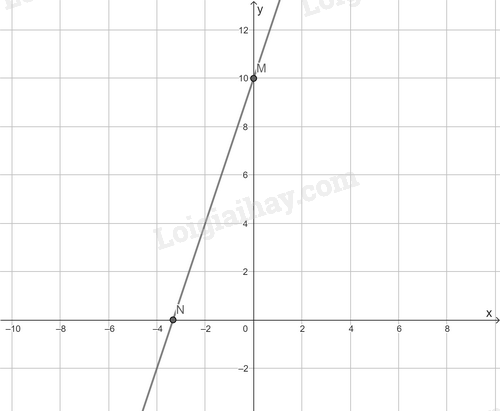
Đồ thị hàm số \(y = 3x + 10\) là đường thẳng đi qua hai điểm \(M;N\).