Hướng dẫn giải TH 3 Bài 2. Các trường hợp đồng dạng của hai tam giác (trang 69, 70) – SGK Toán 8 Chân trời sáng tạo. Tham khảo: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam.
Câu hỏi/Đề bài:
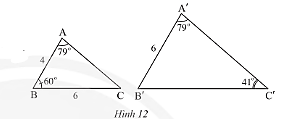
Quan sát Hình 12.
a) Chứng minh \(\Delta ABC\backsim\Delta A’B’C’\).
b) Tính độ dài cạnh \(B’C’\).
Hướng dẫn:
– Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
– Tổng ba góc trong một tam giác có số đo bằng \(180^\circ \).
Lời giải:
a) Xét tam giác \(A’B’C’\) ta có:
\(\widehat {A’} + \widehat {B’} + \widehat {C’} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B’} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B’} = 180^\circ – 79^\circ – 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A’B’C’\) ta có:
\(\widehat A = \widehat {A’} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B’} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A’B’C’\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A’B’C’\) nên \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B’C’}} \Rightarrow B’C’ = \frac{{6.6}}{4} = 9\)
Vậy \(B’C’ = 9\).