Hướng dẫn giải Vận dụng 1 Bài 2. Các trường hợp đồng dạng của hai tam giác (trang 69, 70) – SGK Toán 8 Chân trời sáng tạo. Hướng dẫn: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác.
Câu hỏi/Đề bài:
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có \(AB = 6m,CD = 15m,OD = 8m\) (Hình 13). Tính độ dài đoạn thẳng \(OB\).
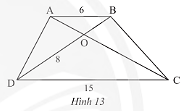
Hướng dẫn:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải:
Vì tứ giác \(ABCD\) là hình thang có \(AB//CD\) nên \(\widehat {BAO} = \widehat {OCD}\) (hai góc so le trong)
Xét tam giác \(ABO\) và tam giác \(CDO\) có:
\(\widehat {BAO} = \widehat {OCD}\) (chứng minh trên)
\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
Do đó, \(\Delta ABO\backsim\Delta CDO\) (g.g)
Ta có: \(\frac{{AB}}{{CD}} = \frac{{OB}}{{OD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{6}{{15}} = \frac{{OB}}{8} \Rightarrow OB = \frac{{6.8}}{{15}} = 3,2\)
Vậy \(OB = 3,2m\).