Giải chi tiết TH 1 Bài 3. Các trường hợp đồng dạng của hai tam giác vuông (trang 73, 74) – SGK Toán 8 Chân trời sáng tạo. Gợi ý: Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai.
Câu hỏi/Đề bài:
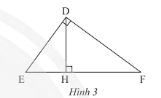
Cho tam giác \(DEF\) vuông tại \(D\) có \(DH\) là đường cao (Hình 3). Chứng minh rằng \(D{E^2} = EH.EF\)
Hướng dẫn:
Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải:
Vì \(DH \bot EF \Rightarrow \widehat {DHE} = 90^\circ \)
Xét tam giác \(DEH\) và tam giác \(FED\) ta có:
\(\widehat E\) chung
\(\widehat {DHE} = \widehat {EDF} = 90^\circ \).
Do đó, \(\Delta DEH\backsim\Delta FED\) (g.g)
Suy ra, \(\frac{{DE}}{{EF}} = \frac{{EH}}{{DE}} \Rightarrow D{E^2} = EF.EH\) (điều phải chứng minh).