Lời giải Hoạt động 2 Bài 4. Hình bình hành – Hình thoi (trang 73, 74, 75, 76) – SGK Toán 8 Chân trời sáng tạo. Tham khảo: Áp dụng tính chất của hai đường thẳng song song.
Câu hỏi/Đề bài:
Cho tứ giác \(ABCD\) có các cạnh đối song song. Gọi \(O\) là giao điểm của hai đường chéo. Hãy chứng tỏ:
– Tam giác \(ABC\) bằng tam giác \(CDA\)
– Tam giác \(OAB\) bằng tam giác \(OCD\)
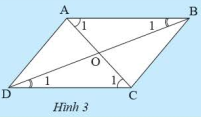
Hướng dẫn:
Áp dụng tính chất của hai đường thẳng song song
Áp dụng trường hợp bằng nhau thứ 2 của tam giác
Lời giải:
Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))
\(AC\) chung
\(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (do \(AD\) // \(BC\))
Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c)
Xét \(\Delta OAB\) và \(\Delta OCD\) ta có:
\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))
AB = CD (do \(\Delta ABC = \Delta CDA\))
\(\widehat {{{\rm{B}}_{\rm{1}}}} = \widehat {{{\rm{D}}_{\rm{1}}}}\) (do \(\Delta ABC = \Delta CDA\))
Suy ra: \(\Delta OAB = \Delta OCD\) (g-c-g)