Giải chi tiết Hoạt động 2 Bài 3. Các trường hợp đồng dạng của hai tam giác vuông (trang 74, 75) – SGK Toán 8 Chân trời sáng tạo. Tham khảo: Sử dụng định lí Py – ta – go.
Câu hỏi/Đề bài:
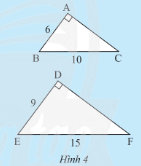
Cho hai tam giác vuông \(ABC\) và \(DEF\) có các kích thước như Hình 4.
a) Hãy tính độ dài cạnh \(AC\) và \(DF\).
b) So sánh các tỉ số \(\frac{{AB}}{{DE}};\frac{{AC}}{{DF}}\) và \(\frac{{BC}}{{EF}}\).
c) Dự đoán sự đồng dạng của hai tam giác\(ABC\) và \(DEF\).
Hướng dẫn:
– Sử dụng định lí Py – ta – go.
– Chứng minh tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh
Lời giải:
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} – {6^2} = 64 \Leftrightarrow AC = 8\).
Xét tam giác \(DEF\) vuông tại \(D\) ta có:
\(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} – {9^2} = 144 \Leftrightarrow DF = 12\).
b) Tỉ số:
\(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\).
Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\).
c) Xét tam giác\(ABC\) và tam giác\(DEF\) có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c)