Giải Hoạt động 2 Bài 2. Các trường hợp đồng dạng của hai tam giác (trang 68, 69) – SGK Toán 8 Chân trời sáng tạo. Hướng dẫn: Sử dụng định lí Thales.
Câu hỏi/Đề bài:
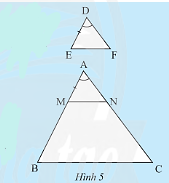
Cho tam giác \(DEF\) và tam giác \(ABC\) có \(DE = \frac{1}{3}AB,DF = \frac{1}{3}AC,\widehat D = \widehat A\) (Hình 5). Trên tia \(AB\), lấy điểm \(M\) sao cho \(AM = DE\). Qua \(M\) kẻ \(MN//BC\left( {N \in AC} \right)\).
a) So sánh \(\frac{{AM}}{{AB}}\) và \(\frac{{AN}}{{AC}}\)
b) So sánh \(AN\) với \(DF\).
c) Tam giác \(AMN\) có đồng dạng với tam giác \(ABC\) không?
d) Dự đoán sự đồng dạng của hai tam giác \(DEF\) và \(ABC\).
Hướng dẫn:
– Sử dụng định lí Thales.
– Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải:
a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).
b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).
Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
d) Dự đoán hai tam giác \(DEF\) và \(ABC\) đồng dạng.