\(\Delta ABC\backsim\Delta DEF \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\). Nếu \(\Delta ABC\backsim\Delta DEF\) theo tỉ số \(k\. Hướng dẫn giải Giải bài 3 trang 70 SGK Toán 8 tập 2- Chân trời sáng tạo – Bài 2. Các trường hợp đồng dạng của hai tam giác. Một công viên có hai đường chạy bộ hình tam giác đồng dạng…
Đề bài/câu hỏi:
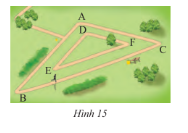
Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m. Cạnh ngắn nhất của con đường bên ngoài là 600 m. Nam chạy bốn vòng bên trong. Hưng chạy hai vòng bên ngoài. So sánh quãng đường chạy của hai bạn.
Hướng dẫn:
\(\Delta ABC\backsim\Delta DEF \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\).
Nếu \(\Delta ABC\backsim\Delta DEF\) theo tỉ số \(k\) thì tỉ số của hai chu vi của hai tam giác đó cũng là \(k\).
Lời giải:
Quan sát hình vẽ ta thấy, cạnh ngắn nhất của tam giác \(ABC\) là cạnh \(AC\);cạnh ngắn nhất của tam giác \(DEF\) là cạnh \(DF\).
Do đó, ta có: \(\frac{{AC}}{{DF}} = \frac{{600}}{{300}} = 2\).
Do đó, tỉ số chu vi của tam giác \(ABC\) và tam giác \(DEF\) là 2.
Chu vi tam giác \(DEF\) là: \(300 + 350 + 550 = 1200m\)
Chu vi tam giác \(ABC\) là: \(1200.2 = 2400m\).
Quãng đường bạn Nam đã chạy là: \(1200.4 = 4800m\)
Quãng đường bạn Hùng đã chạy là: \(2400.2 = 4800m\).
Do đó, hai bạn Nam và Hùng đã chạy hai quãng đường bằng nhau.