Sử dụng định lý Pythagore tính độ dài các cạnh huyền. Giải và trình bày phương pháp giải Giải bài 3 trang 62 SGK Toán 8 – Chân trời sáng tạo – Bài 1. Định lí Pythagore. Lần lượt tính độ dài các cạnh huyền (a), (b), (c), (d) của các tam giác vuông trong Hình 12….
Đề bài/câu hỏi:
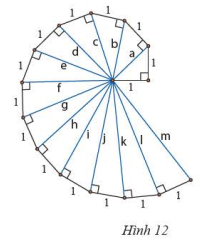
Lần lượt tính độ dài các cạnh huyền \(a\), \(b\), \(c\), \(d\) của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.
Hướng dẫn:
Sử dụng định lý Pythagore tính độ dài các cạnh huyền
Lời giải:
Áp dụng định lý Pythagore vào các tam giác vuông trong hình ta có:
\({a^2} = {1^2} + {1^2} = 1 + 1 = 2\) . Suy ra \(a = \sqrt 2 \)
\({b^2} = {a^2} + {1^2} = 2 + 1 = 3\). Suy ra \(b = \sqrt 3 \)
\({c^2} = {b^2} + {1^2} = 3 + 1 = 4\). Suy ra \(c = \sqrt 4 \)
\({d^2} = {c^2} + {1^2} = 4 + 1 = 5\). Suy ra \(d = \sqrt 5 \)
Dự đoán:
\(e = \sqrt 6 \)
\(f = \sqrt 7 \)
\(g = \sqrt 8 \)
\(h = \sqrt 9 = 3\)
\(i = \sqrt {10} \)
\(k = \sqrt {11} \)
\(l = \sqrt {12} \)
\(m = \sqrt {13} \)