Nếu tam giác vuông này có một góc nhọn bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng. Gợi ý giải Giải bài 14 trang 86 SGK Toán 8 tập 2- Chân trời sáng tạo – Bài tập cuối chương 8. Cho tam giác…
Đề bài/câu hỏi:
Cho tam giác \(ABC\)nhọn có hai đường cao \(BE,CF\) cắt nhau tại \(H\). Chứng minh rằng
a) \(\Delta AEB\backsim\Delta AFC\).
b) \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\).
c) \(\Delta HEF\backsim\Delta HCB\)
Hướng dẫn:
– Nếu tam giác vuông này có một góc nhọn bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
– Nếu \(\Delta ABC\backsim\Delta A’B’C’\) thì \(\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}} = \frac{{BC}}{{B’C’}} = k\).
– Hai tam giác đồng dạng có các góc tương ứng bằng nhau.
Lời giải:
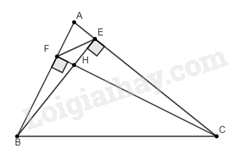
a) Vì \(BE\)là đường cao nên \(\widehat {AEB} = 90^\circ \); vì \(CF\)là đường cao nên \(\widehat {AFC} = 90^\circ \)
Xét tam giác \(AEB\) và tam giác \(AFC\) có:
\(\widehat A\) (chung)
\(\widehat {AEB} = \widehat {AFC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AEB\backsim\Delta AFC\) (g.g).
b) Vì \(\Delta AEB\backsim\Delta AFC\) nên \(\widehat {ACF} = \widehat {ABE}\) (hai góc tương ứng) hay \(\widehat {ECH} = \widehat {FBH}\).
Xét tam giác \(HEC\) và tam giác \(HFB\) có:
\(\widehat {ECH} = \widehat {FBH}\) (chứng minh trên)
\(\widehat {CEH} = \widehat {BFH} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HEC\backsim\Delta HFC\) (g.g).
Suy ra, \(\frac{{HE}}{{HF}} = \frac{{HC}}{{HB}}\) (các cặp cạnh tương ứng tỉ lệ)
Hay \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (điều phải chứng minh).
c) Xét tam giác \(HEF\) và tam giác \(HCB\) có:
\(\widehat {FHE} = \widehat {BHC}\) (hai góc đối đỉnh)
\(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (chứng minh trên)
Suy ra, \(\Delta HEF\backsim\Delta HCB\) (c.g.c).