Nếu tam giác vuông này có một góc nhọn bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng. Phân tích và giải Giải bài 13 trang 86 SGK Toán 8 tập 2- Chân trời sáng tạo – Bài tập cuối chương 8. Người ta đo khoảng cách giữa hai điểm…
Đề bài/câu hỏi:
Người ta đo khoảng cách giữa hai điểm \(D\) và \(K\) ở hai bờ một dòng song (Hình 5). Cho biết \(KE = 90m,KF = 160m\). Tính khoảng cách \(DK\).
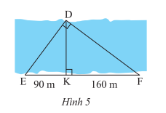
Hướng dẫn:
– Nếu tam giác vuông này có một góc nhọn bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
– Nếu thì \(\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}} = \frac{{BC}}{{B’C’}} = k\).
– Hai tam giác đồng dạng có các góc tương ứng bằng nhau.
Lời giải:
– Xét tam giác \(DEF\) và tam giác \(KDF\) có:
\(\widehat F\) (chung)
\(\widehat {EDF} = \widehat {DKF} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta DEF\backsim\Delta KDF\) (g.g)
Suy ra, \(\widehat E = \widehat {KDF}\) (hai góc tương ứng).
– Xét tam giác \(DEK\) và tam giác \(FDK\) có:
\(\widehat E = \widehat {KDF}\) (chứng minh trên)
\(\widehat {EKD} = \widehat {FKD} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta DEK\backsim\Delta FDK\) (g.g)
Suy ra, \(\frac{{DK}}{{FK}} = \frac{{EK}}{{DK}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(D{K^2} = EK.FK = 90.160 = 14400 \Rightarrow DK = \sqrt {14400} = 120\).
Vậy khoảng cách \(DK = 120m\).