Xác định hai điểm thuộc đồ thị hàm số \(y = – \frac{1}{2}x + 3;y = 2{\rm{x}} – 2\) để vẽ đồ thị hàm số. Vận dụng kiến thức giải Giải bài 4 trang 78 SGK Toán 8 tập 1 – Cánh diều – Bài tập cuối chương 3. Cho hai hàm số:…
Đề bài/câu hỏi:
Cho hai hàm số: \(y = – \dfrac{1}{2}x + 3;y = 2{\rm{x}} – 2\)
a) Vẽ đồ thị của hai hàm số đó trên cùng một mặt phẳng tọa độ.
b) Gọi A, B lần lượt là giao điểm của hai đường thẳng \(y = – \dfrac{1}{2}x + 3;y = 2{\rm{x}} – 2\) với trục hoành và C là giao điểm của hai đường thẳng đó. Tính diện tích của tam giác ABC (đơn vị đo trên các trục là centimét)
Hướng dẫn:
– Xác định hai điểm thuộc đồ thị hàm số \(y = – \frac{1}{2}x + 3;y = 2{\rm{x}} – 2\) để vẽ đồ thị hàm số.
– Xác định tọa độ các điểm A, B, C.
– Tính diện tích của tam giác ABC.
Lời giải:
a) * Vẽ đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\)
Cho x = 0 thì y = 3, ta được điểm P(0; 3) thuộc đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\)
Cho y = 0 thì x = 6 ta được điểm A(6; 0) thuộc đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\)
Vậy đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\) là đường thẳng đi qua hai điểm P(0; 3) và điểm A(6; 0).
* Vẽ đồ thị hàm số y = 2x – 2
Cho x = 0 thì y = -2 ta được điểm Q(0; -2) thuộc đồ thị hàm số y = 2x – 2
Cho y = 0 thì x = 1 ta được điểm B(1; 0) thuộc đồ thị hàm số y = 2x -2
Vậy đồ thị hàm số y = 2x – 2 là đường thẳng đi qua hai điểm Q(0; -2) và B(1; 0)
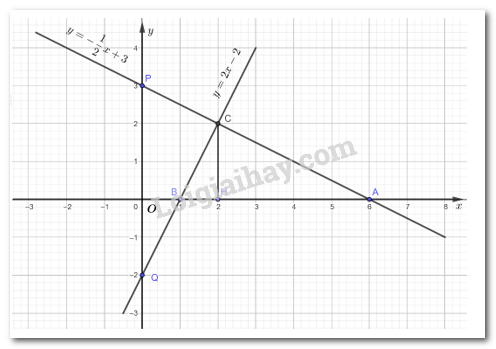
b) Ta có: A là giao điểm của đường thẳng \(y = – \dfrac{1}{2}x + 3\) với trục hoành nên \( – \dfrac{1}{2}x + 3 = 0\) suy ra x = 6 nên A(6; 0)
Ta có: B là giao điểm của đường thẳng y = 2x – 2 với trục hoành nên 2x – 2 = 0 suy ra x = 1 nên B(1; 0)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(y = – \dfrac{1}{2}x + 3\) và y = 2x – 2 ta có:
\(\begin{array}{l} – \dfrac{1}{2}x + 3 = 2{\rm{x}} – 2\\ \Rightarrow 3 + 2 = \dfrac{1}{2}x + 2{\rm{x}}\\ \Rightarrow 5 = \dfrac{5}{2}x\\ \Rightarrow x = 2 \Rightarrow y = 2\end{array}\)
Vì C là hoành độ giao điểm của hai đường thẳng \(y = – \dfrac{1}{2}x + 3\) và y = 2x – 2 nên C(2; 2)
Gọi H là hình chiếu của C lên trục Ox
Khi đó: CH = 2
Mặt khác AB = 5 cm
Diện tích tam giác ABC là; \({S_{ABC}} = \dfrac{1}{2}CH.AB = \dfrac{1}{2}.2.5 = 5\left( {c{m^2}} \right)\)