Lời giải Câu 4 Bài tập cuối Chương 4 (trang 53, 54) – SBT Toán 8 Kết nối tri thức. Tham khảo: Sử dụng kiến thức về định lí Thalès để tìm khẳng định đúng.
Câu hỏi/Đề bài:
Cho hình thang ABCD (AB//DC). Gọi O là giao điểm của AC và BD. Xét các khẳng định sau:
(1) \(\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}}\)
(2) \(OA.OD = OB.OC\)
(3) \(\frac{{AO}}{{AC}} = \frac{{BO}}{{BD}}\)
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3
Hướng dẫn:
Sử dụng kiến thức về định lí Thalès để tìm khẳng định đúng: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải:
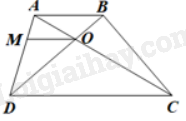
Qua O kẻ OM//AB//CD (M thuộc AD).
Tam giác ADC có: OM//DC nên \(\frac{{OA}}{{OC}} = \frac{{MA}}{{MD}},\frac{{OA}}{{AC}} = \frac{{AM}}{{AD}}\)
Tam giác ADB có: OM//AB nên \(\frac{{OB}}{{OD}} = \frac{{MA}}{{MD}},\frac{{BO}}{{BD}} = \frac{{AM}}{{AD}}\)
Do đó, \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}}\) và \(\frac{{AO}}{{AC}} = \frac{{BO}}{{BD}}\)
Vì \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}}\) nên \(OA.OD = OB.OC\)
Vậy khẳng định (3) và (2) đúng.
Chọn C.