Hướng dẫn giải Câu 3 Bài tập cuối Chương 4 (trang 53, 54) – SBT Toán 8 Kết nối tri thức. Tham khảo: Sử dụng kiến thức về đường trung bình của tam giác để tìm câu đúng.
Câu hỏi/Đề bài:
Cho tam giác ABC cân tại B. Hai trung tuyến AM, BN cắt nhau tại G. Gọi I và K lần lượt là trung điểm của GB, GC. Khẳng định nào đúng?
A. \(MN = \frac{1}{2}AC\)
B. \(BC = \frac{1}{2}IK\)
C. \(MN > IK\)
D. \(MN = IK\)
Hướng dẫn:
Sử dụng kiến thức về đường trung bình của tam giác để tìm câu đúng: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
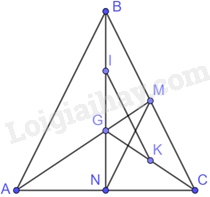
Tam giác ABC cân tại B nên \(AB = BC\) (1)
Tam giác ABC có M, N lần lượt là trung điểm của BC, AC nên MN là đường trung bình của tam giác. Do đó, \(MN = \frac{1}{2}AB\) (2)
Tam giác GBC có I, K lần lượt là trung điểm của BG, GC nên IK là đường trung bình của tam giác. Do đó, \(IK = \frac{1}{2}BC\) (3)
Từ (1), (2) và (3) suy ra: \(MN = IK\)
Chọn D.