Chứng minh \(\Delta CBM = \Delta DCN\) để suy ra \(\widehat {BMC} = \widehat {DNC}\) + Mà \(\widehat {BMC} + \widehat {MCB} = {90^0}\. Vận dụng kiến thức giải Giải bài 9.53 trang 64 sách bài tập toán 8 – Kết nối tri thức với cuộc sống – Bài 36. Các trường hợp đồng dạng của hai tam giác vuông. Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC….
Đề bài/câu hỏi:
Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN.
a) Chứng minh rằng \(CM \bot DN\).
b) Biết \(AB = 4cm,\) hãy tính diện tích tam giác ONC.
Hướng dẫn:
a) + Chứng minh \(\Delta CBM = \Delta DCN\) để suy ra \(\widehat {BMC} = \widehat {DNC}\)
+ Mà \(\widehat {BMC} + \widehat {MCB} = {90^0}\) nên \(\widehat {DNC} + \widehat {MCN} = {90^0}\)
b) + Sử dụng kiến thức định lí Pythagore: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh tam giác đồng dạng: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải:
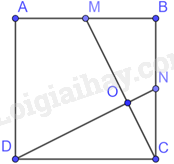
a) Vì ABCD là hình vuông nên \(AB = BC = CD = DA = 4cm\) và \(\widehat {DAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDA} = {90^0}\)
Vì M là trung điểm của AB nên \(AM = MB = \frac{1}{2}AB\)
Vì N là trung điểm của BC nên \(NB = NC = \frac{1}{2}BC\)
Mà \(AB = BC\) nên \(AM = MB = NB = NC\)
Tam giác CBM và tam giác DCN có:
\(\widehat B = \widehat {NCD} = {90^0},MB = NC\left( {cmt} \right),BC = CD\left( {cmt} \right)\)
Do đó, \(\Delta CBM = \Delta DCN\left( {c – g – c} \right)\). Suy ra \(\widehat {BMC} = \widehat {DNC}\)
Mà \(\widehat {BMC} + \widehat {MCB} = {90^0}\) nên \(\widehat {DNC} + \widehat {MCN} = {90^0}\)
Tam giác CON có: \(\widehat {DNC} + \widehat {MCN} = {90^0}\) nên \(\widehat {NOC} = {90^0}\). Do đó, \(CM \bot DN\) tại O
b) Áp dụng định lí Pythagore vào tam giác CND vuông tại C ta có: \(N{D^2} = N{C^2} + C{D^2} = 5N{C^2}.\)
Do đó, \(\frac{{NC}}{{ND}} = \frac{1}{{\sqrt 5 }}\)
Tam giác NOC và tam giác CND có:\(\widehat {NOC} = \widehat {NCD} = {90^0},\widehat {ONC}\;chung\)
Do đó, $\Delta ONC\backsim \Delta CND\left( g-g \right)$
Suy ra: \(\frac{{ON}}{{CN}} = \frac{{OC}}{{CD}} = \frac{{NC}}{{ND}} = \frac{1}{{\sqrt 5 }}\)
Vậy diện tích tam giác ONC là:\(\frac{1}{2}OC.ON = \frac{1}{5}\frac{{CN.CD}}{2} = 0,8\left( {c{m^2}} \right)\)